Produit scalaire canonique

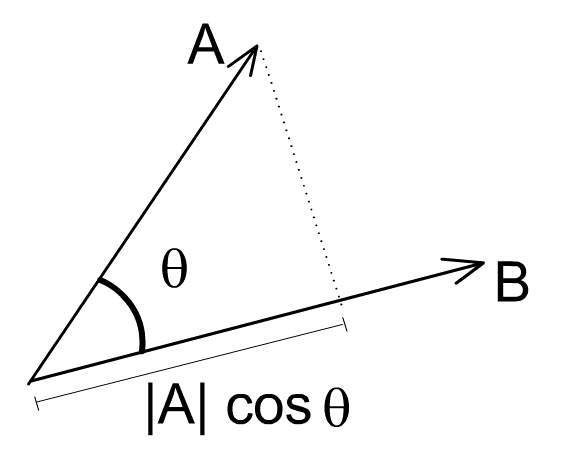
Un produit scalaire canonique est un produit scalaire qui se présente de manière naturelle d'après la manière dont l'espace vectoriel est présenté. On parle également de produit scalaire naturel ou usuel.

Dans

\mathbb {R} ^{n}

On appelle produit scalaire canonique de $\mathbb {R} ^{n}$ l'application qui, aux vecteurs $x=(x_{1},x_{2},\dots ,x_{n})$ et $y=(y_{1},y_{2},\dots ,y_{n})$ de $\mathbb {R} ^{n}$ associe la quantité notée par exemple $x\cdot y$ ou $(x\mid y)$ , définie par :

(x\mid y)=x\cdot y=\sum _{i=1}^{n}x_{i}\,y_{i}

Dans

\mathbb {C} ^{n}

Sur $\mathbb {C} ^{n}$ , on considère le produit scalaire hermitien canonique donné par la formule :

(x\mid y)=\sum _{i=1}^{n}{\bar {x_{i}}}y_{i}

Dans des espaces de fonctions

Dans certains espaces de fonctions (fonctions continues sur un segment ou fonctions de carré sommable, par exemple), le produit scalaire canonique est donné par la formule :

(f\mid g)=\int {\bar {f}}g

où ${\textstyle \int }$ représente une intégration convenable (intégrale de Riemann, de Lebesgue, ...) sur le domaine de définition du produit des deux fonctions.

Dans

{\mathcal {M}}_{m,n}(\mathbb {R} )

Dans l'espace des matrices de taille $m\times n$ à coefficients réels, le produit scalaire usuel est

(M\mid N)=\mathrm {Tr} (M{}^{T}N)=\sum _{i=1}^{m}\sum _{j=1}^{n}M_{i,j}\,N_{i,j}

où $\mathrm {Tr}$ désigne la trace.

Dans des espaces de fonctions

Articles connexes